How can cognitive science principles support the deepening of mathematics education? A team of researchers from Vanderbilt University’s Peabody College of education and human development and Harvard University’s graduate school of education explored how using a basic learning process—comparison—could lead to stronger outcomes for K-12 students in mathematics, and analyzed different approaches for incorporating comparison into curriculum. A summary of the research findings from Peabody College researchers Bethany Rittle-Johnson and Kelley Durkin, in collaboration with Jon Star from Harvard University, was recently published in the December 2020 edition of Current Directions in Psychological Sciences.


When it comes to following mathematical procedures, students often memorize the steps without comprehending the mathematical principles that underlie each one. Asking students to compare and discuss multiple methods for solving the same problem encourages higher order thinking and requires students to demonstrate a deeper understanding of the concepts. According to the research team, comparison is a natural way in which humans learn, noting that, for example, people often compare products to decide which one to buy. Through curricular tools and professional learning opportunities, the researchers supported educators in incorporating this natural thinking process into algebra classrooms.
“We have developed high-quality instructional materials and instructional routines to help teachers use a best-practice in mathematics education in their classrooms,” said Bethany Rittle-Johnson, Anita S. and Antonio M. Gotto Chair in Child Development at Vanderbilt University. “Describing an effective teaching practice is not enough; teachers need materials and routines to support their use of the practice in their classrooms.”
Through their review of past research, the team also sought to understand the types of problems students should compare. They reviewed research on three types of comparison – comparing multiple correct strategies, comparing confusable problem types, and comparing correct and incorrect strategies. They found that incorporating these types of comparison problems resulted in greater conceptual knowledge and procedural flexibility than the control groups.
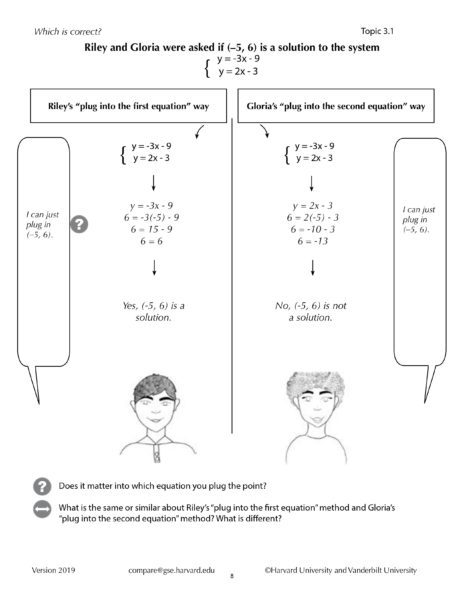
In addition to analyzing the types of problems for students to use comparison strategies, the team sought to understand when in the learning process to use comparison. Specifically, they were curious to determine whether comparison methods should be delayed until learners have some understanding of at least one of the methods. Initially, the team discovered that students were more adept at comparing correct strategies when they had some understanding of one of the strategies. However, the team later found that students were able to effectively use comparison to find similarities and differences between unknown strategies, though this approach required greater support from educators.
Finally, the research team analyzed methods for teaching comparison and provided support to educators to incorporate best practices within their classrooms. The team suggests that educators should make the examples clear and visible to students and present both solutions simultaneously. Additionally, students were most adept at uncovering similarities and differences between strategies when educators used well understood terminology, gestures and visual cues. Moreover, once students identify similarities and differences, educators should use clear prompting questions to encourage explanation of key points and summarize the main points of the comparison after student reflection. To best support educators in incorporating comparison into curriculum, the researchers emphasize the need for high quality, standards-aligned curricular materials and professional learning support. They have developed instructional materials and instructional routines for supporting comparison and discussion of multiple strategies for Algebra I topics.
The team believes this is only the beginning of important research into comparison strategies and pedagogy. Their work has facilitated additional potential research opportunities, such as exploring the impact of comparison strategies on student attitude toward mathematics, or developing teachers’ capacity to detect when their students need additional support.
“We have focused on Algebra I instruction and are eager to develop instructional materials for other math topics like Geometry and to explore additional supports that may be needed to promote comparison and discussion of multiple strategies across diverse learners,” Rittle-Johnson explains.
The research, “How can cognitive-science research help improve education? The case of comparing multiple strategies to improve mathematics learning and teaching” was published in the December 2020 edition of Current Directions in Psychological Sciences. Teachers can learn more about incorporating comparison at the project website.